二分查找、二分答案、三分

二分查找

二分查找主要解决有单调性的序列问题

问题背景

给定一个有序数列，例如{1, 3, 4, 5, 7, 9, 10, 11, 12, 13, 15, 16, 19, 20, 22, 23}，要你通过程序找到$11$这个数所在的位置，如果没找到则输出$-1$

一个比较容易想到的方法是，从前往后枚举，知道当前枚举到的值与$11$相等，则跳出循环

int key = 11, ans = -1;
for (int i = 1; i <= n; i ++ ) {
    if (a[i] == key) {
        ans = key;
        break;
    }
}

不过当数据范围比较大的时候，此时我们的枚举算法就有点力不从心了，请看下面这个场景

例题讲解

P2249 【深基13.例1】查找 - 洛谷

输入 $n$ 个不超过 $10^9$ 的单调不减的（就是后面的数字不小于前面的数字）非负整数 $a_1,a_2,\dots,a_{n}$，然后进行 $m$ 次询问。对于每次询问，给出一个整数 $q$，要求输出这个数字在序列中第一次出现的编号，如果没有找到的话输出 $-1$ 。

如果运用枚举算法，每次查找的时间复杂度是$O(n)$，查找的次数是$m$，所以总的时间复杂度是$O(nm)$，即$10^{11}$这个数量级

可想而知，我们的程序会运行的非常非常慢，此时，就需要用到我们的二分查找算法

由于数列是有序的，则数列要么递增，要么递减，两种的处理方法是类似的，我们先考虑递增的情况

我们的数列类似于下面的这个一次函数，越往左越小，越往右越大

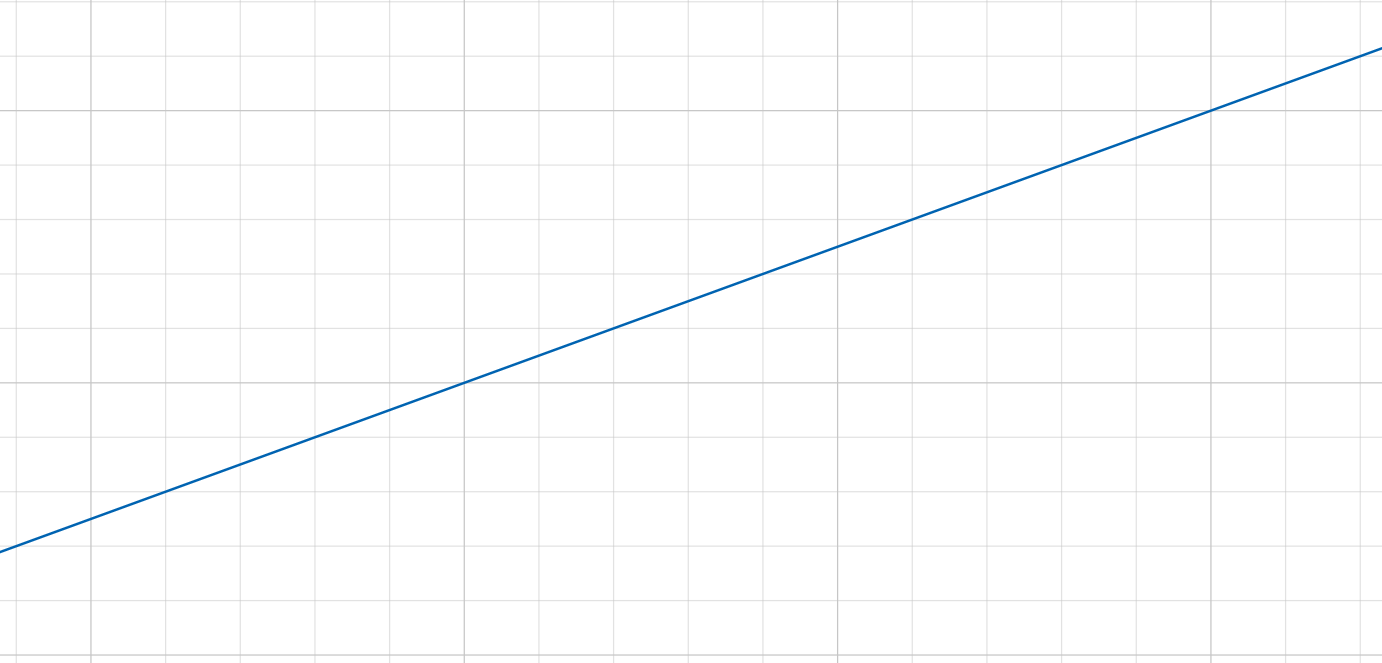
根据越往左越小，越往右越大这个特点，我们可以设计以下算法思路

假设我们要找的数是$key$

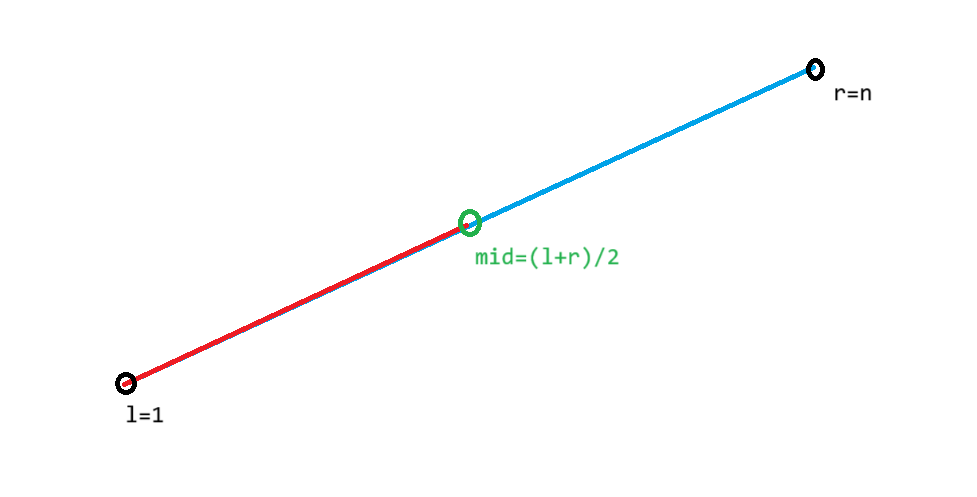
初始状态下，我们声明两个变量，$l$和$r$，并令$l=1$，$r=n$，其中$n$是有序数列的长度，$l$代表目标值所在区间的左端点，$r$代表目标值所在区间的右端点

接下来，我们实现一个迭代过程，令$mid=(l+r)/2$，这样可以得到数列的中值，记为$x$

若$x<key$，则说明中值比目标值小，$mid$以及左边的这段区间中一定没有我们要找的数，下一次迭代之前，我们令$l=mid+1$，将$[l,mid]$这段区间排除在之后的迭代过程中，即排除图中红色的区间，保留蓝色的区间

若$x>key$，则说明中值比目标值大，$mid$以及右边的这段区间中一定没有我们要找到数，下一次迭代之前，我们令$r=mid-1$，将$[mid,r]$这段区间排除在之后的迭代过程中，即排除图中蓝色的区间，保留红色的区间

下面这张图展示了在{1, 3, 4, 5, 7, 9, 10, 11, 12, 13, 15, 16, 19, 20, 22, 23}这个数列中找到数字19时$mid$指针的移动过程

时间复杂度分析

由于每次缩小区间，我们都能减少一半的区间长度，即区间长度的变化过程为
$$
n,\frac{n}{2},\frac{n}{4},\frac{n}{8},…\frac{n}{2^k}
$$
而当区间长度为1的时候，我们的答案就能够确定下来，而上面这个序列的最后一项为$\frac{n}{2^k}$，则根据高中知识，$\frac{n}{2^k}=1$我们能得出$k=log_2(n)$，当然实际情况还需要向上取整，但是数量级是$log_2(n)$这个级别的，所以我们可以说二分查找的时间复杂度为$o(log(n))$

代码实现

int n, m;
int a[N];
void solve() {
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> a[i];
    while (m --) {
        int key;    // 要查找的数
        cin >> key;
        int l = 1, r = n; // 先确定我们要找的区间
        while (l < r) {     // l < r 说明区间长度不为1，没找到答案
            int mid = (l + r) / 2;      // 找到中点
            int x = a[mid];     // 中间值记为x
            if (x < key) {      // 中间值比key小，那么左半区间一定比x小，更加比key小，key不在左半区间
                l = mid + 1;
            } else {            // 中间值大于等于key，答案在mid以及mid的左边，右边区间一定大于等于key
                r = mid;
            }
        }
        // 当循环结束之后，区间长度为1了，说明l和r是相等的
        if (a[l] == key) {
            cout << l << " ";
        } else {
            cout << "-1 ";
        }
    }
}

二分答案

二分答案主要解决答案和枚举值之间有单调性关系的问题和最大值最小或者最小值最大问题

我们来看下面这道题

P1873 砍树 - 洛谷

米尔科的伐木机工作过程如下：米尔科设置一个高度参数 $H$（米），伐木机升起一个巨大的锯片到高度 $H$，并锯掉所有的树比 $H$ 高的部分（当然，树木不高于 $H$ 米的部分保持不变）。米尔科就得到树木被锯下的部分。

例如，如果一行树的高度分别为 $20,15,10,17$，米尔科把锯片升到 $15$ 米的高度，切割后树木剩下的高度将是 $15,15,10,15$，而米尔科将从第 $1$ 棵树得到 $5$ 米木材，从第 $4$ 棵树得到 $2$ 米木材，共 $7$ 米木材。

米尔科非常关注生态保护，所以他不会砍掉过多的木材。这正是他尽可能高地设定伐木机锯片的原因。你的任务是帮助米尔科找到伐木机锯片的最大的整数高度 $H$，使得他能得到木材至少为 $M$ 米。即，如果再升高 $1$ 米锯片，则他将得不到 $M$ 米木材。

问题分析

通过一些简单的计算，我们可以发现，当伐木机的高度越低，砍下的木材的总长度就越多，伐木机的高度越高，砍下的木材的总长度就越少

当伐木机的高度为$0$时，砍下的木材的长度为所有树木高度的总和，当伐木机的高度比最高的数目的高度还要高的时候，产出的木材长度为$0$

我们可以从小到大枚举所有伐木机可能的高度，计算出每个高度下能够砍伐的木材的总长度，找到一个满足木材长度大于等于$m$的锯片高度的最小值即可

并且由于该问题满足：木材的长度随伐木机的高度的升高而减小

故我们可以用二分答案来解决这个问题

则我们可以将答案的区间设定在[0, max]之间，其中$max$为最高的树木的高度，即令l = 0, r = max

计算出中值$mid$之后，通过一个$O(n)$的计算，得出当锯片高度在$mid$的情况下，能砍伐出的木材的总长度为多少

若当前砍伐的木材长度不够$m$，则将二分的区间的左半部分排除，即令l = mid + 1
若当前砍伐的木材长度大于等于$m$，则将二分的区间的右半部分排除，即r = mid，我们不使用r = mid - 1是因为在$mid$的情况下，砍伐的木材长度是符合题目要求的至少需要$m$的木材的这个条件的，所以$mid$是属于答案可能的区间范围内的，不能将它排除在外

通过至多$log_2(max)$次迭代，就能得到最终的答案，花费的总时间复杂度还要加上我们每次check的时间，所以总时间复杂度为$O(nlog(max))$

代码实现

int n, m;
int a[N];

bool check(int x) {
    long long sum = 0;
    for (int i = 1; i <= n; i ++ ) { 
        sum += std::max(a[i] - x, 0);
    }
    return sum >= m;
}
void solve() {
    cin >> n >> m;

    int max = 0;
    for (int i = 1; i <= n; i ++ ) {
        cin >> a[i];
        max = std::max(max, a[i]);
    }

    int l = 0, r = max;
    while (l < r) {
        int mid = (l + r + 1) / 2;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    
    cout << l << "\n";
}

P2678 跳石头 - 洛谷

NOIP2015 Day2T1

一年一度的“跳石头”比赛又要开始了！

这项比赛将在一条笔直的河道中进行，河道中分布着一些巨大岩石。组委会已经选择好了两块岩石作为比赛起点和终点。在起点和终点之间，有 $N$ 块岩石（不含起点和终点的岩石）。在比赛过程中，选手们将从起点出发，每一步跳向相邻的岩石，直至到达终点。

为了提高比赛难度，组委会计划移走一些岩石，使得选手们在比赛过程中的最短跳跃距离尽可能长。由于预算限制，组委会至多从起点和终点之间移走 $M$ 块岩石（不能移走起点和终点的岩石）。

题目分析

问题的重点：我们的目标是让所有相邻的石头中，相隔距离最短的那个石头的间隔距离尽可能长

一个比较容易得出的贪心结论：经过一些简单的思考和计算，我们可以发现，移走更多的石头，肯定能使最短距离更大或者不变

移动石头的方法：对于一个给定的最短距离$x$，我们可以从前往后遍历所有的石头，只要当前石头与前面一块保留的石头的距离比$x$小时，就将其移走，最后统计出一个$cnt$代表移走石头的数量，可以简单思考其正确性，因为当前这块不移走，那么此时就出现了两块距离小于$x$的石头，所以必须移走

问题转化：那么，问题就变成，枚举所有的最短距离，找出所有花费石头数量小于等于$M$时，能找到的最长的最短距离

算法优化：由于，最短距离随着移走的石头数量的增加而增加，则可以用二分答案来解决

代码实现：

int n, m, max;
int a[N];

bool check(int x) {
    int last = 0, cnt = 0;
    for (int i = 1; i <= n; i ++ ) {
        if (a[i] - last < x) {
            cnt ++;
        } else {
            last = a[i];
        }
    }
    if (max - last < x) cnt ++;
    return cnt <= m;
}
void solve() {
    cin >> max >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> a[i];

    int l = 0, r = max;
    while (l < r) {
        int mid = (l + r + 1) / 2;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }

    cout << l << "\n";
}

三分

类比二分算法可以解决单调递增或者单调递减的问题，三分算法可以解决单峰函数问题

需要注意的是，三分算法需要满足单峰函数的极值之外的部分是严格单调的

三分法与二分法的基本思想类似，但每次操作需在当前区间 $[l,r]$（下图中除去虚线范围内的部分）内任取两点 $lmid,rmid(lmid < rmid)$（下图中的两蓝点）。如下图，如果 $f(lmid)<f(rmid)$，则在 $[rmid,r]$（下图中的红色部分）中函数必然单调递增，最小值所在点（下图中的绿点）必然不在这一区间内，可舍去这一区间。反之亦然。

通常情况下，

整数三分时，我们取lmid = (l + r) / 2, rmid = lmid + 1
小数三分时，我们取lmid = (l + r) / 2, rmid = lmid + eps

这样的话，每次排除的区间长度的大小就变成了一半，效率和二分法是一样的

接下来看一道例题

[P3382 三分 - 洛谷

如题，给出一个 $N$ 次函数，保证在范围 $[l, r]$ 内存在一点 $x$，使得 $[l, x]$ 上单调增，$[x, r]$ 上单调减。试求出 $x$ 的值。

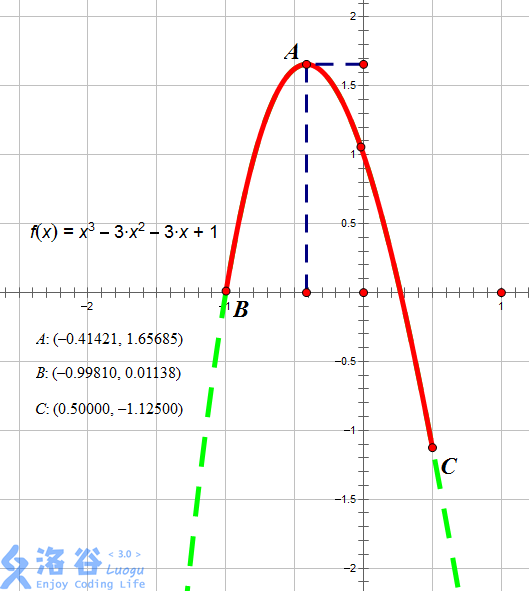
如图所示，红色段即为该函数 $f(x) = x^3 - 3 x^2 - 3x + 1$ 在区间 $[-0.9981, 0.5]$ 上的图像。

当 $x = -0.41421$ 时图像位于最高点，故此时函数在 $[l, x]$ 上单调增，$[x, r]$ 上单调减，故 $x = -0.41421$，输出 $-0.41421$。

代码实现

const int N = 20;
const double eps = 1e-6;

int n;
double a[N];

double calc(double x) {
    double sum = 0;
    for (int i = 1; i <= n; i ++ ) {
        double t = a[i];
        for (int j = 1; j <= n - i; j ++ ) t *= x;
        sum += t;
    }
    return sum;
}
void solve() {
    double l, r;
    cin >> n >> l >> r;
    n ++;
    for (int i = 1; i <= n; i ++ ) cin >> a[i];

    while (l + eps < r) {
        double ml = (l + r) / 2, mr = ml + eps;
        double v1 = calc(ml), v2 = calc(mr);
        if (v1 < v2) l = mr;
        else r = ml;
    }

    cout << std::fixed << std::setprecision(5) << l << "\n";
}

Problem - 2009E - Codeforces

Klee 有一个长度为 $n$ 的数组 $a$ ，其中按顺序包含整数 $[k, k+1, …, k+n-1]$ 。克利希望选择一个索引 $i$ ( $1 \leq i \leq n$ )，使得 $x = |a_1 + a_2 + \dots + a_i - a_{i+1} - \dots - a_n|$ 最小。请注意，对于任意整数 $z$ 来说， $|z|$ 表示 $z$ 的绝对值。

输出 $x$ 的最小可能值。

int n, k;

long long sum(long long a1, long long cnt) {
    return (a1 + a1 + cnt - 1) * cnt / 2;
}

bool check(int ml, int mr) {
    long long s1 = abs(sum(k, ml) - sum(k + ml, n - ml));
    long long s2 = abs(sum(k, mr) - sum(k + mr, n - mr));
    return s1 > s2;
}
void solve() {
    cin >> n >> k;
    int l = 1, r = n;
    while (l < r) {
        int ml = (l + r) / 2, mr = ml + 1;
        if (check(ml, mr)) l = ml + 1;
        else r = mr - 1;
    }

    cout << abs(sum(k, l) - sum(k + l, n - l)) << "\n";
}

代码模板

二分查找库函数

lower_bound( )和upper_bound( )都是利用二分查找的方法在一个排好序的数组中进行查找的。

在从小到大的排序数组中，

lower_bound( begin,end,num)：从数组的begin位置到end-1位置二分查找第一个大于或等于num的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。

upper_bound( begin,end,num)：从数组的begin位置到end-1位置二分查找第一个大于num的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。

在从大到小的排序数组中，重载lower_bound()和upper_bound()

lower_bound( begin,end,num,greater<type>() ):从数组的begin位置到end-1位置二分查找第一个小于或等于num的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。

upper_bound( begin,end,num,greater<type>() ):从数组的begin位置到end-1位置二分查找第一个小于num的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。

代码示例：

#include <bits/stdc++.h>

using namespace std;

int a[] = {0, 1, 2, 3, 3, 3, 4, 5, 6, 7, 8}; // 0-10
//         0  1  2  3  4  5  6  7  8  9  10
int main() {
    int x1 = lower_bound(a, a + 10, 3) - a; // 返回值是3
    int x2 = lower_bound(a, a + 10, 4) - a; // 返回值是6
    cout << x1 << " " << x2 << "\n";

    return 0;
}

整数二分模板

由于整除向下取整的问题，所以有两种写法，防止死循环，重点在于$mid$的取值

while (l < r) {
    int mid = (l + r + 1) / 2;
    if (check(mid)) l = mid;
    else r = mid - 1;
}

while (l < r) {
    int mid = (l + r) / 2;
    if (check(mid)) l = mid + 1;
    else r = mid;
}

小数二分模板

while (l + eps < r) {
    double mid = (l + r) / 2;
    if (check(mid)) r = mid;
    else l = mid;
}

整数三分模板

while (l < r) {
    int ml = (r + l) / 2, mr = ml + 1;
    if (fx(ml) < fx(mr)) l = ml + 1;
    else r = mr - 1;
}

小数三分模板

while (l + eps < r) {
    double ml = (l + r) / 2, mr = ml + eps;
    double v1 = calc(ml), v2 = calc(mr);
    if (v1 < v2) l = mr;
    else r = ml;
}

#算法 #ACM #二分 #二分查找 #二分答案 #三分

二分查找、二分答案、三分

https://www.lry666.cn/posts/20ab/

作者

LRY666

发布于

2024年10月13日

许可协议

双指针上一篇

图的匹配下一篇